FUZZY SET TEORY
- Dasar-Dasar Teori Fuzzy
http://pustaka.unpad.ac.id/wp-content/uploads/2010/07/dasar_dasar_fuzzy_logic.pdf
1. Tujuan
- Memahami defenisi fuzzy set(himpunan fuzzy)
- Memahami fungsi keanggotaan
- Memahami Operator dasar himpunan fuzzy
Himpunan fuzzy adalah himpunan yang keanggotaannya memiliki derajat keanggotaan bilangan. Jika X adalah sekumpulan objek yang dinotasikan himpunan fuzzy A dalam X didefenisikan sebagai pasangan himpunan berorde:
Dimana \mu_{A} (x) disebut funggi keanggotaan (membership fuction) untuk himpunan fuzzy A. Pemetaan MF tiap elemen X pada suatu derajat keanggotaan antara 0 dan 1. Berikut ini beberapa macam himpunan Fuzzy:
- Himpunan fuzzy dengan universe diskrit tak berorde
- Himpunan fuzzy dengan universe diskrit berorde
- Himpunan fuzzy dengan universe kontinyu
3. Fungsi Keanggotaan
Fungsi keanggotaan (membership function) adalah suatu kurva yang menunjukkan pemetaan titik-titik input data kedalam nilai keanggotaan yang memiliki interval antara 0 sampai 1.
Terdapat dua defenisi fungsi keanggotaan (membership function) untuk himpunan fuzzy: numerical dan functional.
Numerical merupakan pernyataan tingkat dari fungsi keanggotaandari himpunan fuzzy dinyatakan dengan vektor bilangan, seperti: 5,10,15,dan sebagainya
functional merupakan menentukan fungsi keanggotaan dari himpunan fuzzy dalam pernyataan analitik yang menyatakan tingkat keanggotaan untuk setiap elemen yang ditentukan dalam himpunan universal of discourse to be calculate, seperti:muda, parubaya, tua
Standar atau shapes dari fungsi keanggotaan adalah kesepakatan yang digunakan untuk dasar himpunan fuzzy pada universal U dari bilangan riil fungsi keanggotaan yang harus digunakan adalah: (a) S-function, (b) pii-fungtion, (c) triangular form, (d) trapezoid form, dan eksponensial form, klir dan folger.
3.1 Representasi linier
Pada representasi linear, pemetaan input ke derajat keanggotaannya dapat digambarkan sebagai suatu garis lurus. Bentuk ini paling sederhana dan menjadi pilihan yang baik untuk mendekati suatu konsep yang kurang jelas.
- Representasi linear naik, yaitu kenaikan himpunan dimulai dari nilai domain yang memiliki nilai keanggotaan nol [0] bergerak ke kanan menuju ke nilai domain yang memiliki derajat keanggotaan yang lebih tinggi
-Representasi linear turun, yaitu garis lurus yang dimulai dari nilai domain dengan derajat keanggotaan tertinggi pada sisi kiri, kemudian bergerak turun ke nilai domain yang memiliki derajat keanggotaan lebih rendah
3.2 Representasi Kurva Segitiga
Representasi kurva segitiga, pada dasarnya adalah gabungan antara dua representasi linear (representasi linear naik dan representasi linear turun),
3.3 Representasi Kurva Trapesium
Representasi kurva trapesium pada dasarnya seperti bentuk kurva segitiga,hanya saja ada beberapa titik yang memiliki nilai keanggotaan 1 (satu),
a. Operator AND
Operator ini berhubungan dengan operasi interseksi pada himpunan firestrengh sebagai hasil operasi dengan operator AND diperoleh dengan mengambil nilai keanggotaan terkecil antar elemen pada himpunan-himpunan yang bersangkutan
b. Operator OR(Y)
Operator ini berhubungan dengan operasi union pada himpunan firestrengh sebagai hasil operasi operator OR diperoleh dengan mengambil nilai keanggotaan terbesar atar elemen pada himpunan-himpunan yang bersangkutan
c. Operator NOT(Y)
Operator ini berhubungan dengan operasi komplemen pada himpunan firestrengh sebagai hasil operasi operator NOT diperoleh dengan megurangkan nilai keanggotaan elemen pada himpunan-himpunan yang bersangkutan dari 1.
1. Himpunan fuzzy ditulis sebagai pasangan berurutan, dengan elemen pertama menunjukkan nama elemen dan elemen kedua menunjukkan nilai keanggotaannya
misal:
Misalkan industri kendaraan bermotor ingin merancang dan memproduksi sebuahmobil yang nyaman untuk digunakan keluarga yang besar. Ada 5 model yangtelah dirancang dan ditunjukkan dalam variabel X = {1, 2, 3, 4,5}, dengan 1adalah desain mobil ke-1, dan seterusnya. Himpunan fuzzy à yang merupakan himpunan “mobil yang nyaman digunakan untuk keluarga yang besar” dapatditulis sebagai: à = {(1; 0,6); (2; 0,3); (3; 0,8); (4; 0,2); (5; 0,1)}
2. Apabila semesta X adalah himpunan yang diskret, maka himpunan fuzzy à dapat dinotasikan sebagai:
6. Video
7. Referensi
- Dasar-Dasar Teori Fuzzy
http://pustaka.unpad.ac.id/wp-content/uploads/2010/07/dasar_dasar_fuzzy_logic.pdf
- https://repository.usm.ac.id/files/skripsi/C41A/2014/C.431.14.0029/C.431.14.0029-05-BAB-II-20180524123829-PENENTUAN-KUALITAS-PRODUK-BOTOL-DI-PT-MAPAN-DJAYA-MENGGUNAKAN-METODE-MAMDANI-.pdf





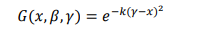

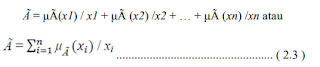
Tidak ada komentar:
Posting Komentar